Açılar

AÇI NEDİR?

Başlangıç noktaları ortak olan iki ışının birleşim kümesine açı denir.

Işınların ortak noktasına açının köşesi, ışınlara ise açının kolları veya açının kenarları denir.

Örneğin şekildeki açı O açısı, AOB açısı veya BOA açısı olarak isimlendirilir.

Sembolle \(\mathrm A\widehat{\mathrm O}\mathrm B\), \(\mathrm B\widehat{\mathrm O}\mathrm A\), veya \(\widehat{\mathrm O}\) şeklinde gösterilir.

Bu açının köşesi O noktasıdır ve açının kolları [OA ve [OB ışınlarıdır.

Açının Ölçüsü

Tam bir çember 360 eş parçaya bölündüğünde bu parçalardan birini gören merkez açının (köşesi çemberin merkezinde yer alan açı) ölçüsü 1 derecedir ve sembolle 1° şeklinde gösterilir.

Şekilde AOB açısının ölçüsü 35 derecedir. Sembolle \(\mathrm m(A\widehat{\mathrm B}\mathrm C)\) = 35°

AÇI ÇEŞİTLERİ

Dar Açı

Ölçüsü 0° ile 90° arasında olan açıya dar açı denir.

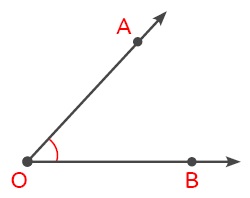
ÖRNEK: Ölçüsü 2x − 10° olan bir açı dar açı ise x’in değer aralığını bulalım.

0° < 2x − 10° < 90°
10° < 2x < 80°
5° < x < 40°

Dik Açı

Ölçüsü 90° olan açıya dik açı denir.

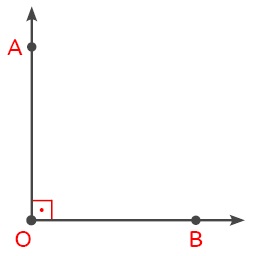
ÖRNEK: Ölçüsü 4x + 40° olan bir açı dik açı ise x’in değerini bulalım.

4x + 40° = 90°
4x = 50°
x = 12,5°

Geniş Açı

Ölçüsü 90° ile 180° arasında olan açıya geniş açı denir.

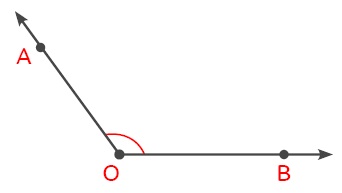
ÖRNEK: Ölçüsü 8x + 10° olan bir açı geniş açı ise x’in alabileceği en büyük tam sayı değerini bulalım.

90° < 8x + 10° < 180°
80° < 8x < 170°
10° < x < 21,25°
x’in alabileceği en büyük tam sayı değeri 21’dir.

Doğru Açı

Ölçüsü 180° olan açıya doğru açı denir.

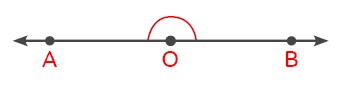
Tam Açı

Ölçüsü 360° olan açıya tam açı denir.

KOMŞU, TÜMLER, BÜTÜNLER ve TERS AÇILAR

Komşu Açılar

Birer kolu ortak olan açılara komşu açılar denir.

ÖRNEK: Aşağıdaki AOB açısı ile BOC açısının [OC kenarı ortak olduğu için bu iki açı komşudur.

Tümler Açılar

Ölçüleri toplamı 90° olan iki açıya tümler açılar denir.

ÖRNEK: Ölçüsü 40° olan bir açıyla ölçüsü 50° olan bir açı birbirinin tümleridir.

Komşu olan tümler açılara komşu tümler açılar denir.

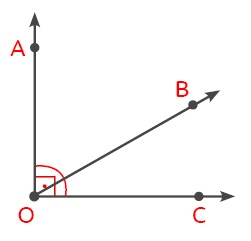
ÖRNEK: Aşağıdaki AOB açısı ile BOC açısı hem komşu hem de tümler oldukları için bu iki açı komşu tümler açıdır.

ÖRNEK: Tümleri kendisinin 4 katı olan açı kaç derecedir bulalım.

Açıya x denirse tümleri 4x olur.
x + 4x = 90°
5x = 90°
x = 18°

Bütünler Açılar

Ölçüleri toplamı 180° olan iki açıya bütünler açılar denir.

ÖRNEK: Ölçüsü 105° olan bir açıyla ölçüsü 75° olan bir açı birbirinin bütünleridir.

Komşu olan bütünler açılara komşu bütünler açılar denir.

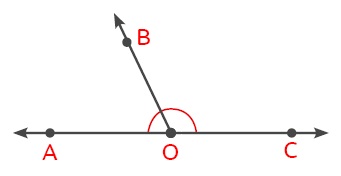
ÖRNEK: Aşağıdaki AOB açısı ile BOC açısı hem komşu hem de bütünler oldukları için bu iki açı komşu bütünler açıdır.

ÖRNEK: Bütünleri tümlerinin 3 katından 50° az olan açı kaç derecedir bulalım.

Açıya x denirse tümleri 90° − x, bütünleri 180° − x olur.
180° − x = 3.(90° − x) − 50°
180° − x = 270° − 3x − 50°
2x = 40°
x = 20°

Ters Açılar

İki doğrunun kesişmesiyle oluşan açılardan komşu olmayanlara ters açılar denir ve ölçüleri birbirine eşittir.

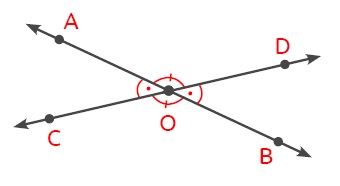
ÖRNEK: Aşağıdaki AOC açısı ile DOB açısı, AOD açısı ile COB açısı ters açılardır.

EŞ AÇILAR VE AÇIORTAY

Eş Açılar

Ölçüleri birbirine eşit olan açılara eş açılar denir. Bir A açısı ile B açısı eş ise bu durum sembolle \(\widehat{\mathrm A}\cong\widehat{\mathrm B}\) şeklinde gösterilir.

ÖRNEK: Aşağıdaki AOC açısı ile DOB açısı ters açılar ise x kaç derecedir bulalım.

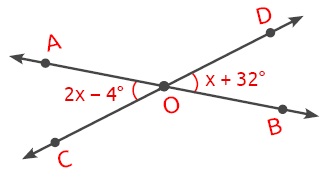
Ters açıların ölçüleri birbirine eşit olduğu için AOC açısı ile DOB açısı eş açılardır.

2x − 4° = x + 32°
x = 36°

Açıortay

Bir açıyı iki eş açıya bölen ışına açıortay denir. Şekilde [OC, AOB açısını iki eş açıya böldüğünden açıortaydır.