Üçgende Açı Kenar Bağıntıları

Bir üçgende ölçüsü küçük olan açının karşısında kısa kenar, büyük açının karşısında uzun kenar vardır.

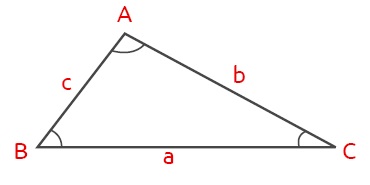
s(\(\widehat A\)) > s(\(\widehat B\)) > s(\(\widehat C\)) ise a > b > c olur.

ÖRNEK: Aşağıdaki üçgenin kenar uzunluklarını sıralayalım.

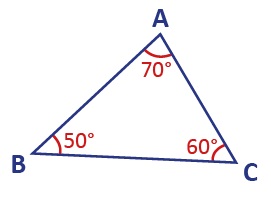
Açıların ölçülerine göre sıralanışı A > C > B olduğu için bu açıların karşılarındaki kenarların uzunlukları da aynı sıralamaya sahip olacaktır.

|BC| > |AB| > |AC| sıralaması elde edilir.

ÖRNEK: Aşağıdaki üçgenin açılarını ölçülerine göre sıralayalım.

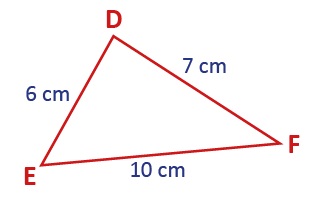
Kenar uzunluklarının sıralanışı |EF| > |DF| > |DE| olduğu için bu kenarların karşılarındaki açılar da aynı sıralamaya sahip olacaktır.

s(\(\widehat D\)) > s(\(\widehat E\)) > s(\(\widehat F\)) sıralaması elde edilir.

NOTLAR:
► Bir üçgende ölçüleri eşit açıların karşısındaki kenarların uzunlukları birbirine eşittir.
► Dik açılı üçgende, diğer açılar dar açı olacağı için, dik açının karşısındaki kenar (hipotenüs) en uzun kenardır.
► Geniş açılı üçgende, diğer açılar dar açı olacağı için, geniş açının karşısındaki kenar en uzun kenardır.

ÖRNEK: Aşağıdaki şekildeki en uzun kenarı bulalım.

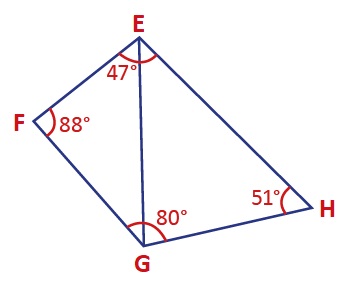
Bu tarz sorularda şekildeki en büyük açının karşısındaki kenarın en uzun olduğunu düşünmek gibi bir yanılgıya düşülmemelidir. Her üçgen kendi içinde değerlendirilir ve o üçgendeki en büyük açının karşısındaki kenar o üçgenin en uzun kenarıdır. Bir üçgenin en uzun kenarı, başka bir üçgenin en kısa kenarı olabilir.

Örneğin şekildeki en büyük açının (88°) karşısındaki [EG] kenarı sağdaki üçgende 51° nin karşısındadır. Sol üçgenin en uzun kenarı sağdaki üçgenin ortanca kenarıdır. [EH] kenarı ise ondan daha uzundur. Kenar sıralaması şu şekildedir:

Soldaki üçgen: |FE| < |FG| < |EG|

Sağdaki üçgen: |GH| < |EG| < |EH|

Cevap: [EH]

ÖRNEK: Aşağıdaki şekildeki en uzun kenarı bulalım.

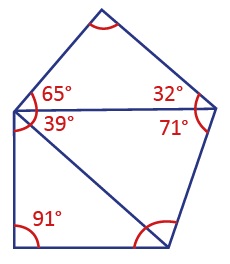
Üçgenlerin kenarları uç uca birleşip yeni bir doğru parçası oluşturmadığı için bu soruyu çözmede farklı ve pratik bir yol kullanabiliriz. Ok çizme yöntemi de diyebileceğimiz bu yöntemde her üçgenin en büyük açısından karşısındaki kenara doğru bir ok çizilir. (Eğer soruda en kısa kenar soruluyorsa bu durumda en küçük açılara bu işlem uygulanır.) Tüm oklar takip edilerek cevap bulunur.

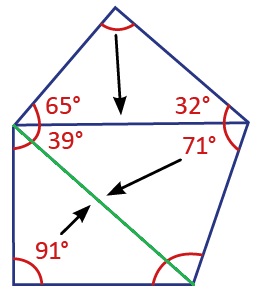
Üstteki üçgenin oku ortadaki üçgeni, ortadaki üçgenin oku ve sol alttaki üçgenin oku ise yeşil kenarı işaret ettiği için bu şekildeki en uzun kenar yeşil kenardır.

ÖRNEK: Aşağıdaki şekildeki en uzun kenarı bulalım.

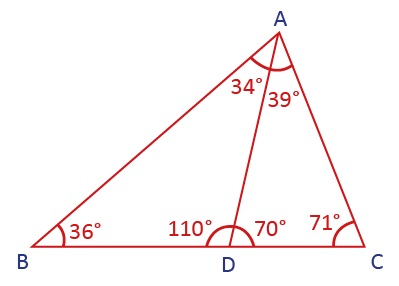
Bu şekilde BDA açısı ile ADC açısı doğru açı oluşturduğu için ABD üçgeni ile ADC üçgeninin birleşimi olan şekil de bir üçgendir (ABC üçgeni).

Ok çizme yöntemi ile kolaylıkla bulunabilen [AB] kenarı doğru cevap değildir çünkü büyük üçgende (ABC) kenar uzunlukları sıralaması |BC| > |AB| > |AC| dir.

Bu yüzden cevap [BC] olur.