TANIM VE KAVRAMLAR
a,b,c \(\in\) R ve a,b \(\neq\) 0 olmak üzere ax + by + c = 0 şeklinde ifade edilebilen denklemlere x ve y değişkenine bağlı birinci dereceden iki bilinmeyenli denklemler denir.
Bir denklemin birinci dereceden iki bilinmeyenli denklem olabilmesi için iki değişken içermesi ve değişkenlerin kuvvetinin 1 olması gerekir.
► x + 2y = 16 ve y = 3x − 5 denklemleri birinci dereceden iki bilinmeyenli denklemlerdir.
Birinci dereceden iki bilinmeyenli denklemleri sağlayan x ve y gerçek sayıları (x, y) sıralı ikilisi olarak yazılır. Bu sıralı ikililerden her biri denklemin çözüm kümesinin bir elemanıdır.
ÖRNEK: x + y = 3 denklemini sağlayan (x, y) sıralı ikililerini bulalım.
Denklemde bir değişkene değer vererek diğerinin değeri bulunabilir. Bu örnekte x’e değerler vererek y değerlerini bulalım.
x = −10 için y = 13 olur: (−10, 13)
x = 0 için y = 3 olur: (0, 3)
x = 12 için y = −9 olur: (12, −9)
şeklinde sonsuz sıralı ikili bulabiliriz.
BİRİNCİ DERECEDEN İKİ BİLİNMEYENLİ DENKLEMLERİN GRAFİKLERİ
Birinci dereceden iki bilinmeyenli denklemlerin grafikleri koordinat sisteminde bir doğru belirtir. Bu doğru, denklemi sağlayan (x, y) sıralı ikililerinin temsil ettiği noktalardan geçer.
Denklem Grafiği Nasıl Çizilir?
Bir denklemin grafiğinin çizilebilmesi için bu doğrunun geçtiği en az 2 nokta bulunmalıdır. Bunun için sıralı ikililer elde edilmelidir. Genelde denklemde x’e sıfır değeri verilerek doğrunun y eksenin kestiği nokta, y’ye sıfır verilerek doğrunun x eksenini kestiği noktanın bulunması tercih edilir.
ÖRNEK: 2x − 3y = 6 denkleminin grafiğini çizelim.
Doğrunun eksenleri kestiği noktaları buluruz. Bu noktaları koordinat sisteminde işaretleyerek grafiği çizeriz.
| x | y | (x , y) |
| 0 | −2 | (0 , −2) |
| 3 | 0 | (3 , 0) |

ÖRNEK: y = −2x denkleminin grafiğini çizelim.
Bu doğru orijinden geçer. Geçtiği ikinci noktayı isteğimize göre belirleyebiliriz. Bu noktaları koordinat sisteminde işaretleyerek grafiği çizeriz.
| x | y | (x , y) |
| 0 | 0 | (0 , 0) |
| 2 | −4 | (2 , −4) |
ÖRNEK: y = 4 denkleminin grafiğini çizelim.
Denklemde x değişkeni bulunmadığı için x’in her değeri için y = 4’tür. İki nokta belirleyip grafiği çizeriz.
| x | y | (x , y) |
| −2 | 4 | (−2 , 4) |
| 3 | 4 | (3 , 4) |

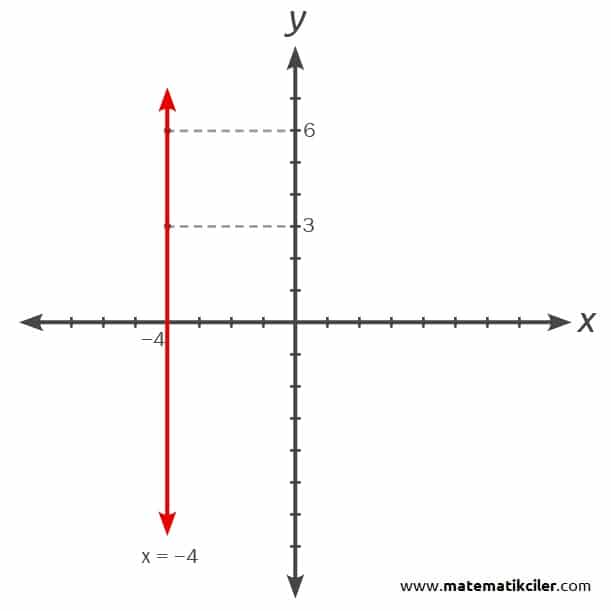
ÖRNEK: 2x + 3 = −5 denkleminin grafiğini çizelim.
Denklemde x’i yalnız bırakırsak x = −4 elde ederiz, y değişkeni bulunmadığı için y’nin her değeri için x = −4’tür.
| x | y | (x , y) |
| −4 | 3 | (−4 , 3) |
| −4 | 6 | (−4 , 6) |
DENKLEM SİSTEMLERİ
a,b,c,d,e,f \(\in\) R ve a,b,c,d \(\neq\) 0 olmak üzere
ax + by + c = 0
dx + ey + f = 0
denklemlerinden oluşan sisteme x ve y değişkenine bağlı birinci dereceden iki bilinmeyenli denklem sistemi denir. Her iki denklemi de sağlayan (x, y) sıralı ikililerinin kümesine denklem sisteminin çözüm kümesi denir.
Birinci dereceden iki bilinmeyenli denklemlerin grafikleri koordinat sisteminde doğru belirttikleri için denklem sisteminin çözüm kümesi bu doğruların kesişim noktalarıdır. Burada karşımıza üç farklı durum çıkar:
► İki doğru bir noktada kesişebilir.
► İki doğru paralel olabilir.
► İki doğru çakışık olabilir.
Denklem sisteminin çözüm kümesini, denklem sistemindeki denklemlerin katsayılarından yorumlayabiliriz.
ÇÖZÜM KÜMESİ – KATSAYI İLİŞKİSİ
ax + by + c = 0 ve dx + ey + f = 0 denklemlerinden oluşan denklem sisteminin kökleri ve dolayısıyla çözüm kümesi katsayıların (a,b,c,d,e,f) oranı ile ilişkilidir.
1) Çözüm Kümesinin Tek Elemanlı Olması
ax + by + c = 0
dx + ey + f = 0 denklem sisteminde
\(\frac{a}{d}\neq\frac{b}{e}\) ise denklem sistemini sağlayan yalnız bir (x,y) ikilisi vardır.
Doğrular bir noktada kesişir.
ÖRNEK: Aşağıdaki denklem sisteminin çözüm kümesini inceleyelim.
6x + 4y = 7
2x + 5y = 10
\(\frac{6}{2}\neq\frac{4}{5}\) olduğu için çözüm kümesi bir elemanlıdır, doğrular kesişir.
2) Çözüm Kümesinin Boş Küme Olması
ax + by + c = 0
dx + ey + f = 0 denklem sisteminde
\(\frac{a}{d}=\frac{b}{e}\neq\frac{c}{f}\) ise denklem sistemini sağlayan (x,y) ikilisi yoktur. Çözüm kümesi boş kümedir. Ç = \(\varnothing\)
Doğrular paraleldir, kesişmez.
ÖRNEK: Aşağıdaki denklem sisteminin çözüm kümesini inceleyelim.
x − 2y = 8
3x − 6y = −5
\(\frac{1}{3}=\frac{-2}{-6}\neq\frac{8}{-5}\) olduğu için çözüm kümesi boş kümedir doğrular paraleldir. Ç = \(\varnothing\)
3) Çözüm Kümesinin Sonsuz Elemanlı Olması
ax + by + c = 0
dx + ey + f = 0 denklem sisteminde
\(\frac{a}{d}=\frac{b}{e}=\frac{c}{f}\) ise denklem sistemini sağlayan sonsuz (x,y) ikilisi vardır.
Doğrular çakışıktır.
ÖRNEK: Aşağıdaki denklem sisteminin çözüm kümesini inceleyelim.
x − 2y = 5
−3x + 6y = −15
\(\frac{1}{-3}=\frac{-2}{6}=\frac{5}{-15}\) olduğu için çözüm kümesi sonsuz elemanlıdır, doğrular çakışıktır.
DENKLEM SİSTEMİ ÇÖZÜMÜ
Denklem sistemlerinin çözüm kümesini bulmak için yerine koyma, yok etme ya da grafik çizme yöntemi kullanılır.
1) Yerine Koyma Yöntemi
1.ADIM: Denklem sistemindeki denklemlerden herhangi birinde, değişkenlerden herhangi biri eşitliğin bir tarafında yalnız bırakılarak diğeri cinsinden eşiti bulunur.
2.ADIM: Yalnız bıraktığımız değişkenin eşiti diğer denklemde yerine konularak değişkenlerden birinin değeri bulunur.
3.ADIM: Diğer değişkenin değeri ise herhangi bir denklemde bulduğumuz değişkenin değerini yerine yazarak elde edilir.
ÖRNEK: Aşağıda verilen denklem sistemini yerine koyma yöntemini kullanarak adım adım çözelim.
x + y = 3
2x − y = 0
İlk adım olarak herhangi bir denklemde herhangi bir değişken yalnız bırakılır. Biz 2. denklemde y’yi yalnız bırakmayı tercih ettik ve y = 2x eşitliğini olduğunu bulduk.
2x − y = 0
y = 2x
2. adım olarak diğer denklemde y yerine 2x yazdık ve x = 1 değerini elde ettik.
x + y = 3
x + 2x = 3
3x = 3
x = 1
Son adımda herhangi bir denklemde x yerine 1 yazılır. Biz y = 2x denkleminde x yerine 1 koyarak y = 2 değerini bulduk.
y = 2x
y = 2.1
y = 2
Ç = { (1, 2) }
Çözüm kümesi boş küme (grafikleri paralel) olan denklemlerden oluşan denklem sistemleri yerine koyma yöntemiyle çözüldüğünde 0 = 5 gibi yanlış eşitlikler elde edilir, değişken değeri bulunamaz.
Benzer şekilde çözüm kümesi sonsuz elemanlı (grafikleri çakışık) olan denklemlerden oluşan denklem sistemleri yerine koyma yöntemiyle çözüldüğünde 0 = 0 gibi doğru eşitlikler elde edilir, değişken değeri bulunamaz.
2) Yok Etme Yöntemi
1.ADIM: Denklem sisteminde herhangi bir değişkenin katsayıları denklemi genişletme veya sadeleştirme yöntemi ile birbirinin toplama işlemine göre tersi (ters işaretlisi) olacak hale getirilir.
2.ADIM: Denklemler taraf tarafa toplanarak bu değişken yok edilir olur ve bir bilinmeyenli denklem elde edilir. Bu denklem çözülerek değişkenlerden birinin değeri bulunur.
3.ADIM: Bulunan değer verilen denklemlerden herhangi birinde yerine konularak diğer değişkenin değeri bulunur.
ÖRNEK: Aşağıdaki denklem sistemini yok etme yöntemini kullanarak adım adım çözelim.
2x + y = 5
3x − 2y = −3
İlk adım olarak yok edeceğimiz değişkeni seçmemiz gerekir. Biz y’i yok etmeyi tercih ettik ve üstteki denklemi 2 ile genişlettik. Sonuç olarak denklemlerde y’nin katsayıları 2 ve −2 oldu.
2x + y = 5 / .2
3x − 2y = −3
4x + 2y = 10
3x − 2y = −3
2. adım olarak iki denklemi tarafa tarafa toplarız ve bir bilinmeyenli denklem elde ederiz. Bu denklemde değişkenin değerini x = 1 buluruz.
4x + 2y = 10
3x − 2y = −3
7x = 7
x = 1
Son olarak herhangi bir denklemde x yerine 1 yazarız ve y’yi buluruz. Biz ilk denklemde x’i yerine yazmayı tercih ettik ve y = 3 bulduk.
2x + y = 5
2.1 + y = 5
y = 3
Ç = { (1, 3) }
Çözüm kümesi boş küme (grafikleri paralel) olan denklemlerden oluşan denklem sistemleri yok etme yöntemiyle çözüldüğünde 0 = 5 gibi yanlış eşitlikler elde edilir, değişken değeri bulunamaz.
Benzer şekilde çözüm kümesi sonsuz elemanlı (grafikleri çakışık) olan denklemlerden oluşan denklem sistemleri yok etme yöntemiyle çözüldüğünde 0 = 0 gibi doğru eşitlikler elde edilir, değişken değeri bulunamaz.
3) Grafik Çizerek Yorumlama
Denklem sisteminin çözümü, denklem sistemini oluşturan denklemlerin grafiklerinin kesişim noktasının koordinatlarıdır.
ÖRNEK: Aşağıdaki denklem sistemini denklemlerin grafikleri yardımıyla çözelim.
x + y = 1
2x + y = −2
x + y = 1 denkleminde:
x = 0 için y = 1 olur: (0 , 1)
y = 0 için x = 1 olur: (1, 0)
2x + y = −2 denkleminde:
x = 0 için y = −2 olur: (0 , −2)
y = 0 için x = −1 olur: (−1, 0)
Bu noktaları kullanarak denklemlerin grafiği çizilir. Doğruların kesiştiği (−3,4) noktası denklem sisteminin çözümüdür.

Çözüm kümesi boş küme olan denklemlerden oluşan denklem sistemlerinin grafikleri çizildiğinde doğruların paralel oldukları görülür.
Benzer şekilde çözüm kümesi sonsuz elemanlı olan denklemlerden oluşan denklem sistemlerinin grafikleri çizildiğinde doğruların çakışık olduğu görülür.
| ÖNCEKİ KONU | SONRAKİ KONU |
| Birinci Dereceden Bir Bilinmeyenli Eşitsizlikler | Birinci Dereceden İki Bilinmeyenli Eşitsizlikler |
matematikciler.com olarak ziyaretçilerimize ücretsiz ve nitelikli içerikler sunmak için yoğun çaba sarfediyoruz. Bu emeğin korunması adına bu konu anlatımının izinsiz yayınlanması yasaktır!

