Fraktal parçalanmış ya da kırılmış anlamına gelen Lâtince fractuuss kelimesinden gelmiştir. İlk olarak 1975’de Polonya asıllı matematikçi Benoit Mandelbrot tarafından ortaya atıldığı varsayılır.
Kendi kendini tekrar eden ama sonsuza kadar küçülen şekilleri, kendine benzer bir cisimde cismi oluşturan parçalar ya da bileşenler cismin bütününü inceler.
Düzensiz ayrıntılar ya da desenler giderek küçülen ölçeklerde yinelenir ve tümüyle soyut nesnelerde sonsuza kadar sürebilir; tam tersi de her parçanın her bir parçası büyütüldüğünde, gene cismin bütününe benzemesi olayıdır.
FRAKTAL NEDİR?
Fraktaller, matematiksel bir fonksiyonun sonucunun aynı fonksiyona tekrar girdi olarak verilmesi ile oluşturulur. Matematikte bu tip ilerlemeye iterasyon adı verilir.
1915 lerde Fransız matematikçi Julia, kendi ismiyle anılacak olan bu akışı bulduğunda, henüz bu yaklaşımla ilgili büyük rakamlı hesaplamalar yapılamıyordu.
f(x) = x2 + 2 … x = 1 ise, sonuç = 3
f(x) = x2 + 2 … x = 3 ise, sonuç = 11
f(x) = x2 + 2 … x = 121 ise, sonuç = 123
f(x) = x2 + 2 … x = 123 ise, sonuç = 15131
…
Fraktallerin tam olarak anlaşılması için bilgisayarın icadı gerekecektir.
İlk bulunmasından yaklaşık elli yıl sonra matematikçi Mandelbrot tarafından yapılan çalışmalar Julia’nın çalışmalarına hayat vermiştir.
DOĞADA FRAKTAL ÖRNEKLERİ
Doğada görülebilen fraktallara örnek olarak bazı bitkilerin yapısı verilebilir. Fraktala en çok verilen örnek eğrelti otudur. Eğrelti otunun her yaprağının üzerinde yine küçük küçük yapraklar vardır. Ayrıca bulutlarda, dağlarda, ağaçlarda, yıldırımda, kalp ritminde, akciğerdeki bronşlarda ve daha bir çok yerde fraktal görmek mümkündür.
Fraktallar ile ilgili daha fazla bilgi sahibi olmak için Fraktallar Belgeselini izleyebilirsiniz.
Fraktal Örnekleri ve Fraktal Resimleri










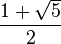 olur.
olur.











