Üçgende Açılar

ÜÇGEN NEDİR?

Düzlemde doğrusal olmayan üç noktanın ikişer ikişer birleştirilmesi ile elde edilen geometrik şekle üçgen denir.

[AB] \(\cup\) [BC] \(\cup\) [AC] = ABC üçgeni

Üçgenin Temel Elemanları

Üçgenin temel elemanları köşeleri, kenarları ve açılarıdır.

• A, B, C noktaları üçgenin köşeleridir.
• [AB], [BC] ve [AC] üçgenin kenarlarıdır.
• a, b, c üçgenin iç açılarıdır.
• x, y, z üçgenin dış açılarıdır.

Açıortay, kenarortay, yükseklik ve kenar orta dikme üçgenin yardımcı elemanlarıdır.

ÜÇGENDE AÇI ÖZELLİKLERİ

Bir üçgenin iç açılarının ölçüleri toplamı 180° dir.

Şekildeki üçgende iç açılar toplamı a + b + c = 180° dir.

► Bu ifadenin doğruluğunu göstermek için A köşesinden [BC] kenarına paralel çizilir. a açısına komşu olan açılar, iç ters açılardan dolayı, b ve c’dir. Bu şekilde a, b ve c doğru açı oluşturur ve toplamları 180 derece olur.

Bir üçgenin dış açılarının ölçüleri toplamı 360° dir.

Şekildeki üçgende dış açılar toplamı x + y + z = 360° dir.

► Bu ifadenin doğruluğu şu şekilde gösterilebilir:
a + x = 180° (Doğru açı)
b + y = 180° (Doğru açı)
c + z = 180° (Doğru açı)
x + y + z + a + b + c = 540° (Eşitlikler taraf tarafa toplanır.)
x + y + z + 180° = 540° (Üçgenin iç açıları toplamı a + b + c yerine 180° yazılır.)
x + y + z = 360° bulunur.

Bir üçgende bir dış açının ölçüsü kendine komşu olmayan iki iç açının ölçülerinin toplamına eşittir.

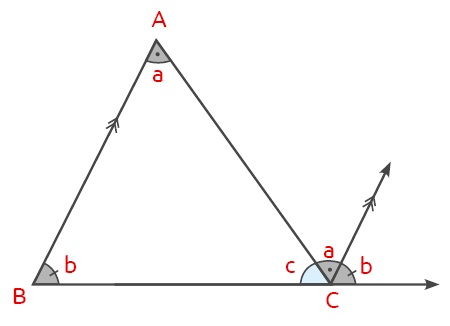
Şekildeki üçgende C köşesindeki dış açı diğer iki köşedeki a ve b açılarının toplamına eşittir.

► Bu ifadenin doğruluğunu göstermek için C köşesinden [AB] kenarına paralel çizilir. c açısına komşu olan açı iç ters açılardan dolayı a’ya eşittir. C köşesindeki diğer açı yöndeş açılardan dolayı b’ye eşittir. Bu şekilde C köşesindeki dış açının a+b’ye eşit olduğu görülür.

► Bu ifadenin doğruluğu cebirsel olarak da gösterilebilir. C köşesindeki dış açı x olsun.
c + x = 180° ifadesinde x yalnız bırakılır:
x = 180° − c olur.
Üçgenin iç açıları toplamı a+b+c = 180° olduğu için yukarıdaki ifadede 180° yerine a+b+c yazılabilir.
x = a + b + c − c
x = a + b olarak bulunur.

AÇILARINA GÖRE ÜÇGENLER

Dar Açılı Üçgen

Tüm açıları dar açı olan üçgenlere dar açılı üçgen denir.

Şekildeki DAR üçgeni dar açılı üçgendir.

Dik Açılı Üçgen

Bir açısı dik açı olan üçgenlere dik açılı üçgen denir.

Şekildeki DİK üçgeni dik açılı üçgendir.

Geniş Açılı Üçgen

Bir açısı geniş açı olan üçgenlere geniş açılı üçgen denir.

Şekildeki GNŞ üçgeni geniş açılı üçgendir.

KENARLARINA GÖRE ÜÇGENLER

Çeşitkenar Üçgen

Tüm kenar uzunlukları birbirinden farklı olan üçgenlere çeşitkenar üçgen denir.

Çeşitkenar üçgenin açılarının ölçüleri de birbirinden farklıdır.

İkizkenar Üçgen

İki kenar uzunluğu eşit olan üçgenlere ikizkenar üçgen denir.

İkizkenar üçgende eşit uzunluktaki kenarların birleştiği köşedeki açıya (A) tepe açısı, diğer iki açıya (B ve C) taban açıları denir. Taban açılarının ölçüleri birbirine eşittir.

Eşkenar Üçgen

Tüm kenar uzunlukları eşit olan üçgenlere eşkenar üçgen denir.

Eşkenar üçgende tüm açıların ölçüleri birbirine eşittir ve 60° dir.