ARALIK KAVRAMI
Sayı doğrusu üzerinde birbirinden farklı iki noktanın arasındaki tüm gerçek sayılardan oluşan alt kümeye aralık denir.
Aralıklar, uç noktaların verilen kümeye dâhil olup olmamasına göre farklı şekilde adlandırılır. a ve b gerçek sayıları aralıkların uç noktaları olmak üzere aralıklar [a,b], (a,b), [a,b), (a,b] şeklinde gösterilir.
KAPALI ARALIK
Her iki uç noktasının da aralığa dâhil edildiği kümelere kapalı aralık denir.
A = { x | a \(\leq\) x \(\leq\) b ve a, b, x \(\in\) R } kümesi bir kapalı aralık belirtir ve bu aralık [a,b] ile ifade edilir.
Kapalı aralığın sayı doğrusunda gösterimi aşağıdaki gibidir.

AÇIK ARALIK
Her iki uç noktasının da aralığa dâhil edilmediği kümelere açık aralık denir.
A = { x | a \(\lt\) x \(\lt\) b ve a, b, x \(\in\) R } kümesi bir kapalı aralık belirtir ve bu aralık (a,b) ile ifade edilir.
Açık aralığın sayı doğrusunda gösterimi aşağıdaki gibidir.

YARI AÇIK ARALIK
Uç noktalarından yalnız birinin aralığa dâhil edildiği kümelere yarı açık aralık denir.
A = { x | a \(\leq\) x \(\lt\) b ve a, b, x \(\in\) R } ve A = { x | a \(\lt\) x \(\leq\) b ve a, b, x \(\in\) R } kümeleri birer yarı açık aralık belirtir, bu aralıklar sırasıyla [a,b) ve (a,b] ile ifade edilir.
Yarı açık aralığın sayı doğrusunda gösterimi aşağıdaki gibidir.

ALTTAN SINIRSIZ ARALIKLAR
adece üstten sınırlı olan aralıklara alttan sınırsız aralık denir.
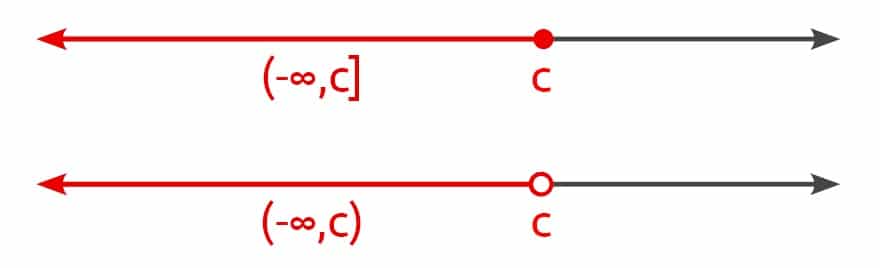
A = { x | x \(\leq\) c ve c, x \(\in\) R } kümesinin belirttiği aralık (−∞,c] ile ifade edilir.
A = { x | x \(\lt\) c ve c, x \(\in\) R } kümesinin belirttiği aralık (−∞,c) ile ifade edilir.
Alttan sınırsız aralıkların sayı doğrusunda gösterimi aşağıdaki gibidir.
ÜSTTEN SINIRSIZ ARALIKLAR
Sadece alttan sınırlı olan aralıklara üstten sınırsız aralık denir.
A = { x | d \(\leq\) x ve d, x \(\in\) R } kümesinin belirttiği aralık [d,∞) ile ifade edilir.
A = { x | d \(\lt\) x ve d, x \(\in\) R } kümesinin belirttiği aralık (d,∞) ile ifade edilir.
Üstten sınırsız aralıkların sayı doğrusunda gösterimi aşağıdaki gibidir.

| ÖNCEKİ KONU | SONRAKİ KONU |
| Periyodik Olarak Tekrar Eden Durumlar | Birinci Dereceden Bir Bilinmeyenli Denklemler |
matematikciler.com olarak ziyaretçilerimize ücretsiz ve nitelikli içerikler sunmak için yoğun çaba sarfediyoruz. Bu emeğin korunması adına bu konu anlatımının izinsiz yayınlanması yasaktır!
