BU KONUDA ÖĞRENECEKLERİMİZ:
✓ Çokgenlerde köşegen
✓ Çokgende iç ve dış açı
✓ Köşegen formülleri, açı formülleri
ÇOKGENLER
Bir düzlemde herhangi ikisi doğrusal olmayan en az üç noktanın ardışık bir şekilde birleştirilmesiyle oluşan kapalı geometrik şekle çokgen denir.
► Çokgenler kenar sayılarına göre adlandırılır.
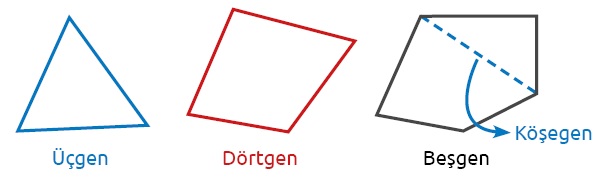
► Bir çokgenin ardışık olmayan herhangi iki köşesini birleştiren doğru parçalarının her birine köşegen adı verilir.
ÇOKGEN FORMÜLLERİ
Bir Köşeden Çizilen Köşegen Sayısı
n kenarlı bir çokgenin bir köşesinden (n – 3) tane köşegen çizilebilir.
n kenarlı bir çokgenin n tane köşesi vardır. Bir köşe seçtiğimizde bu köşeden kendisine ve 2 komşusuna köşegen çizemeyiz. Bu yüzden köşe sayısından 3 çıkartırız.
ÖRNEK: Aşağıdaki görseldeki mavi çizgiler bir köşeden çizilen köşegenleri göstermektedir.

Üçgenin köşegeni yoktur. Dörtgenin bir köşesinden 1, beşgenin 2, altıgenin 3 köşegen çizilebilir.
ÖRNEK: Bir onbeşgenin bir köşesinden çizilebilen köşegen sayısını bulalım.
Bir köşeden çizilen köşegen sayısı formülü (n – 3)’tür. Soruda kenar sayısı verildiği için n = 15 alırız. Cevabı da 15 – 3 = 12 olarak buluruz.
ÖRNEK: Bir köşesinden çizilebilen köşegen sayısı 20 olan çokgen kaç kenarlıdır bulalım.
Bir köşeden çizilen köşegen sayısı formülü (n – 3)’tür. Soruda bir köşesinden çizilen köşegen sayısı verildiği için (n – 3)’ü 20’ye eşitleriz ve kenar sayısını buluruz.
n – 3 = 20
n = 23
Bir Köşeden Çizilen Köşegen ile Oluşan Üçgen Sayısı
n kenarlı bir çokgenin bir köşesinden köşegenler çizilerek (n – 2) tane üçgen elde edilebilir.
Bir köşeden çizilen köşegenlerle oluşan üçgen sayısı köşegen sayısından bir fazla olduğu için (n – 3)’e 1 ekleriz ve formülü (n – 2) buluruz.
ÖRNEK: Aşağıdaki görselde bir köşeden çizilen köşegenlerle oluşan üçgen sayıları verilmiştir.

Bir köşeden köşegenler çizilince dörtgende 2, beşgende 3, altıgende 4 tane üçgen oluşur.
ÖRNEK: Bir ongenin bir köşesinden çizilebilen köşegenlerle oluşan üçgen sayısını bulalım.
Bir köşeden çizilen köşegenlerle oluşan üçgen sayısı formülü (n – 2)’dir. Soruda kenar sayısı verildiği için n = 10 alırız. Cevabı da 10 – 2 = 8 olarak buluruz.
ÖRNEK: Bir köşesinden çizilebilen köşegenlerle oluşan üçgen sayısı 15 olan çokgen kaç kenarlıdır bulalım.
Bir köşeden çizilen köşegen sayısı formülü (n – 2)’dir. Soruda bir köşesinden çizilen köşegenlerle oluşan üçgen sayısı verildiği için (n – 2)’yi 15’e eşitleriz ve kenar sayısını buluruz.
n – 2 = 15
n = 17
Toplam Köşegen Sayısı
n kenarlı bir çokgenin toplam \(\frac{n.(n – 3)}{2}\) tane köşegeni vardır.
n tane köşenin her birinden (n – 3) tane köşegen çizilebilir. Bu çizimler sonucunda n.(n – 3) kere çizim yapılmış olur. Ancak her bir köşegenin iki ucundan da çizim yapıldığı için toplam köşegen sayısı n.(n – 3)’ün yarısıdır.
ÖRNEK: Aşağıdaki görselde çokgenlerin tüm köşegenleri çizilmiştir.
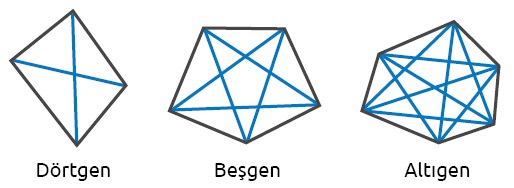
Üçgenin köşegeni yoktur. Dörtgenin 2, beşgenin 5, altıgenin 9 köşegeni vardır.
ÖRNEK: Bir onikigenin kaç köşegeni vardır bulalım.
Köşegen sayısı formülü \(\frac{n.(n – 3)}{2}\)‘dir. Soruda kenar sayısı verildiği için n = 12 alırız. Cevabı da \(\frac{12.9}{2}\) = 54 olarak buluruz.
ÖRNEK: Köşegen sayısı 27 olan çokgen kaç kenarlıdır bulalım.
Köşegen sayısı formülü \(\frac{n.(n – 3)}{2}\)‘dir. Soruda köşegen sayısı verildiği için \(\frac{n.(n – 3)}{2}\)‘yi 27’ye eşitleriz ve kenar sayısını buluruz.
\(\frac{n.(n – 3)}{2}\) = 27
n.(n – 3) = 54
n = 9
İç Açı ile Dış Açı Toplamı
Bir çokgenin aynı köşesine ait iç açısı ile dış açısının ölçüleri toplamı 180° dir.
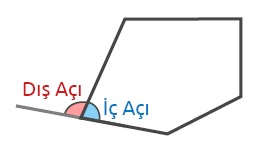
Çokgende kenarların kesişmesi ile iç bölgede oluşan açılara iç açı denir. Bir kolu kenarın uzantısı olan ve iç açılara komşu olan açılara ise dış açı denir.
Çokgende İç Açılar Toplamı
n kenarlı bir çokgenin iç açılarının ölçüleri toplamı (n – 2).180° dir.
Bir çokgende bir köşeden köşegenlerin çizilmesiyle (n – 2) tane üçgen oluşuyordu. Bu üçgenlerin her birinin iç açıları ölçüleri toplamı 180° dir ve bu açılar çokgenin iç açılarını oluşturur. Bu yüzden çokgenin iç açılarının ölçüleri toplamını bulurken (n – 2) ile 180° çarpılır.
ÖRNEK: Bir altıgenin iç açıları ölçüleri toplamı kaç derecedir bulalım.
İç açıları toplamı formülü (n – 2).180°’dir. Soruda kenar sayısı verildiği için n = 6 alırız. Cevabı da 4.180° = 720° olarak buluruz.
ÖRNEK: İç açıları ölçüleri toplamı 1080° olan çokgen kaç kenarlıdır bulalım.
İç açıları toplamı formülü (n – 2).180°’dir. Soruda iç açıları ölçüleri toplamı verildiği için (n – 2).180°’yi 1080’e eşitleriz ve kenar sayısını buluruz.
(n – 2).180° = 1080°
n – 2 = 6
n = 8
Çokgende Dış Açılar Toplamı
Tüm çokgenlerin dış açılarının ölçüleri toplamı 360° dir.
ÖRNEK: Bir onbeşgenin dış açıları ölçüleri toplamı kaç derecedir bulalım.
Tüm çokgenlerin dış açıları ölçüleri toplamı 360° olduğu için onbeşgenin de dış açıları ölçüleri toplamı 360° dir.
| Üçgen | Dörtgen | Beşgen | Altıgen | Yedigen | Sekizgen | |
|---|---|---|---|---|---|---|
| Köşe/Kenar Sayısı | 3 | 4 | 5 | 6 | 7 | 8 |
| Bir Köşeden Çizilen Köşegen Sayısı | – | 1 | 2 | 3 | 4 | 5 |
| Bir Köşeden Çizilen Köşegenlerle Oluşan Üçgen Sayısı | 1 | 2 | 3 | 4 | 5 | 6 |
| Toplam Köşegen Sayısı | – | 2 | 5 | 9 | 14 | 20 |
| İç Açıları Toplamı | 180° | 360° | 540° | 720° | 900° | 1080° |
| Dış Açıları Toplamı | 360° | 360° | 360° | 360° | 360° | 360° |
KONUYU PEKİŞTİRMEK İÇİN:
İLGİLİ KAZANIM TESTİ BAĞLANTISI
KONU KAZANIMLARI
BU KONUYLA İLGİLİ KAZANIMLAR:
✓ Çokgenlerin köşegenlerini, iç ve dış açılarını belirler; iç açılarının ve dış açılarının ölçüleri toplamını hesaplar.
| ÖNCEKİ KONU | SONRAKİ KONU |
| Paralel İki Doğrunun Bir Kesenle Yaptığı Açılar | Düzgün Çokgenler |
