Üçgenin Alanı

BU KONUDA ÖĞRENECEKLERİMİZ:
✓ Üçgende yükseklik
✓ Üçgenin alanı nasıl bulunur?
✓ Üçgenin alan formülü

ÜÇGENİN YÜKSEKLİĞİ

Üçgenin bir köşesinden karşı kenarına çizilen dikmeye yükseklik denir ve yükseklik h harfiyle gösterilir. Üçgenin üç farklı yüksekliği vardır. Yüksekliğin çizildiği kenara ise taban adı verilir.

Yükseklik çizerken gönye (dik üçgen şeklindeki araç) veya bir köşesi dik olan araçlar (örneğin kitap, uç kutusu vs.) kullanılabilir.

Dar Açılı Üçgende Yükseklik

Üç açısı da 90 dereceden küçük olan üçgenlere dar açılı üçgen denir. Dar açılı üçgenlerde üç yükseklik de üçgenin içinde yer alır.

Yukarıdaki görselde ABC üçgeninin:
C köşesinden [AB] kenarına çizilen yükseklik [CP],
A köşesinden [CB] kenarına çizilen yükseklik [AR],
B köşesinden [AC] kenarına çizilen yükseklik [BS]’dir.

Dik Açılı Üçgende Yükseklik

Bir açısı 90 derece olan üçgenlere dik açılı üçgen denir. Dik açılı üçgenlerde bir yükseklik üçgenin içinde yer alır, diğer iki yükseklik ise üçgenin dik kenarlarıdır.

Yukarıdaki görselde ABC üçgeninin:
A köşesinden [BC] kenarına çizilen yükseklik [AP],
C köşesinden [AB] kenarına çizilen yükseklik [CA],
B köşesinden [AC] kenarına çizilen yükseklik [BA]’dir.

Geniş Açılı Üçgende Yükseklik

Bir açısı 90 dereceden büyük olan üçgenlere geniş açılı üçgen denir. Geniş açılı üçgenlerde bir yükseklik üçgenin içinde, iki yükseklik üçgenin dışında yer alır.

Yukarıdaki görselde ABC üçgeninin:
A köşesinden [BC] kenarına çizilen yükseklik [AS],
C köşesinden [AB] kenarının uzantısına çizilen yükseklik [CP],
B köşesinden [AC] kenarının uzantısına çizilen yükseklik [BR]’dir.

ÜÇGENİN ALANI

Üçgenin alanı, bir kenarının uzunluğu ile o kenara ait yüksekliğin uzunluğunun çarpımının yarısına eşittir.

Dik kenarlarının uzunlukları bilinen bir dik üçgenin alanı, dik kenar uzunluklarının çarpımının yarısına eşittir.

ÖRNEK: Aşağıda verilen üçgenlerin alanlarını bulalım.

► KLM dik üçgeninde [LM] taban kabul edilirse taban 8 cm, bu tabanın yüksekliği de 5 cm olur.

KLM üçgeninin alanı = \(\frac{8.5}{2}\) = \(\frac{40}{2}\) = 20 cm²

► ABC üçgeninde [BC] taban kabul edilirse taban 10 cm, bu tabanın yüksekliği de 7 cm olur.

ABC üçgeninin alanı = \(\frac{10.7}{2}\) = \(\frac{70}{2}\) = 35 cm²

► PRS üçgeninde [RS] taban kabul edilirse taban 7 cm, bu tabanın yüksekliği de 6 cm olur.

PRS üçgeninin alanı = \(\frac{7.6}{2}\) = \(\frac{42}{2}\) = 21 cm²

ÖRNEK: Aşağıda noktalı kağıtta verilen üçgenlerin alanlarını bulalım.

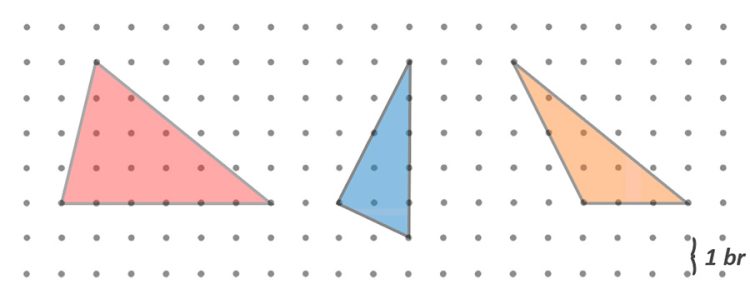
► Kırmızı üçgende alt kenar taban kabul edilirse taban 6 birim, üst köşeden bu tabana çizilecek yükseklik de 4 birim olur.

Kırmızı üçgeninin alanı = \(\frac{6.4}{2}\) = \(\frac{24}{2}\) = 12 br²

► Mavi üçgende sağ kenar taban kabul edilirse taban 5 birim, sol köşeden bu tabana çizilecek yükseklik de 2 birim olur.

Mavi üçgeninin alanı = \(\frac{5.2}{2}\) = \(\frac{10}{2}\) = 5 br²

► Turuncu üçgende alt kenar taban kabul edilirse taban 3 birim, üst köşeden bu tabanın uzantısına çizilecek yükseklik de 4 birim olur.

Turuncu üçgeninin alanı = \(\frac{3.4}{2}\) = \(\frac{12}{2}\) = 6 br²

ÖRNEK: Aşağıdaki ABC dik üçgeninin dik kenarlarının uzunlukları ve diğer kenarın yüksekliğinin uzunluğu verilmiştir. Buna göre verilmeyen kenar uzunluğunu bulalım.

ABC üçgeninin alanını dik kenar uzunluklarını kullanarak bulabiliriz.

ABC üçgeninin alanı = \(\frac{15.20}{2}\) = \(\frac{300}{2}\) = 150 cm²

[BC] kenarını taban kabul edersek bu tabanın yüksekliği 12 cm olur. Bu yüzden [BC] kenarının uzunluğu ile 12’nin çarpımının yarısı ABC üçgeninin alanına eşittir.

\(\frac{|BC|.12}{2}\) = 150
|BC| . 6 = 150
|BC| = 25 cm buluruz.

KONUYU PEKİŞTİRMEK İÇİN:

matematikciler.com olarak ziyaretçilerimize ücretsiz ve nitelikli içerikler sunmak için yoğun çaba sarfediyoruz. Bu emeğin korunması adına bu konu anlatımının izinsiz yayınlanması yasaktır!